Current research
 y
principal research area is Dynamical Systems. I am also interested in
applications of its methods to problems in other fields, such as Hyperbolic
Geometry and Number Theory.
Currently I am working on three problems that belong to completely different areas.
y
principal research area is Dynamical Systems. I am also interested in
applications of its methods to problems in other fields, such as Hyperbolic
Geometry and Number Theory.
Currently I am working on three problems that belong to completely different areas.

The theory of dynamical systems itself attracts me as an area of mathematics closely connected to physics. Thus, my PhD Thesis is dedicated to the kinematic fast dynamo problem, which belongs to the area of magnetohydrodynamics. Magnetic dynamo theory involves the study of the generation of magnetic field in large astrophysical objects as planets and stars [M78]. It attempts to gain some understanding of the non-diffusive processes that might be involved by addressing the problem of what sort of fluid motions can induce exponential growth of magnetic field at high magnetic Reynolds number. This is one of a large class of singular problems with important physical implications for which there is a need for a better understanding of the limiting behaviour of complicated processes.
The question [VZ72] asks, whether there exist a divergence-free velocity field v in a compact domain M such that the energy E(t)= ∥B(t)∥2L1 of the magnetic field B(t) grows exponentially in time for some initial field B(0)=B0 and for arbitrarily low diffusivity?
The problem has a long history. Numerical evidence supporting positive answer for certain chaotic flows as well as negative results have been obtained, an overview can be found in [AK98], see [JP14] and [KKL10] for recent results. Fluid flows that give a positive answer to this problem are called fast dynamo flows. The case of special interest are stationary velocity fields in three-dimensional domains.
We have constructed a provisional fluid flow and established that the statement holds true for the induced action by Poincaré map on vector fields on the plane. Currently we are working towards a full solution of the kinematic fast dynamo problem in its original form.
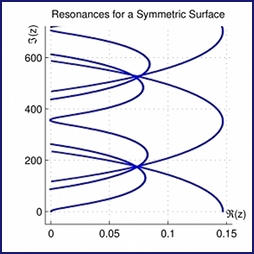
The class of questions I am interested in lie at the intersection between hyperbolic geometry, number theory, and dynamical systems. These areas are naturally connected by dynamical zeta functions [R76]. The goal is to connect algebraic properties of the zeta function (distribution of zeros) to the geometry of the associated hyperbolic surface. Unlike the dynamo problem, this topic is rather new and conjectures arose from numerical experiments that were impossible before computer era.
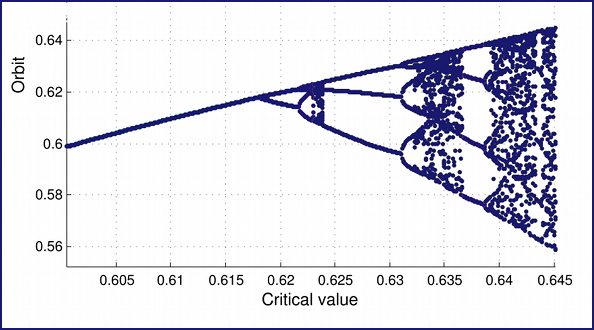
It is well known that the study of one-dimensional systems is essential for understanding higher dimensional models [L95], [S10]. The project aims to understand topological properties of unimodal maps with a non-symmetric singularity. Wandering intervals play an important role in topological aspects of one-dimensional dynamics [MS93] and are essential for studying topological conjugacy. The existence of wandering intervals for smooth maps is now completely understood. However, the question [BM98] whether wandering intervals may or may not exist for a map which is smooth except at the critical points, where the local symmetry is broken, remains open. We have constructed numerically a close approximation to an infinitely renormalizable map, which is likely to have a wandering interval.
| [AK98] | Arnold, V. I. and Khesin, B. A. Topological methods in hydrodynamics. Applied Mathematical Sciences, v. 125, Springer‒Verlag, 1998. |
| [BM98] | Blokh, A. M. and Misiurewicz, M. Collet-Eckmann maps are unstable. Comm. Math. Phys., 191(1): 61—70, 1998. |
| [MS93] | de Melo, W. and van Strien, S. One‒dimensional dynamics, vol. 25 of Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)]. Springer-Verlag, Berlin, 1993. |
| [JG14] | Jones, S. E. and Gilbert, A. D. Dynamo action in the ABC flows using symmetries. Geophys. Astrophys. Fluid Dyn. 108 (2014), no. 1, 83—116. |
| [KKL10] | Kogan, V. R., Kolokolov, I. V., and Lebedev, V. V. Kinematic magnetic dynamo in a random flow with strong average shear. J. Phys. A 43 (2010), no. 18, 182–201. |
| [L95] | Lyubich, M. On the borderline of real and complex dynamics. Proc. ICM, Z\"urich 1994. Birkh\"auser 1995, v. 2, 1203–1215. |
| [M78] | Moffatt, H. K. Magnetic field generation in electrically conducting fluids (1978), 343pp. |
| [R76] | Ruelle, D. Zeta‒functions for expanding maps and Anosov flows. Invent. Math. 34 (1976) 231–242. |
| [VZ72] | Vainshtein, S. I. and Zeldovich, Ya. B. Origin of magnetic fields in astrophysics. Soviet Phys. Usp. 15, (1972), 159–172. |
| [S10] | van Strien, S. One‒dimensional dynamics in the new millennium, Disc. Cont. Dynam. Syst. A 27, 2 (2010), 557–588. |