The Hausdorff dimension of certain subsets of the real line, described in terms of the continued fraction expansions of their elements, plays an important role in problems from number theory, such as Zaremba’s conjecture (here is a masterfully written expository paper by A. Kontorovich) and the structure of the Markov and Lagrange spectra (here is beautiful introduction to the subject by C. Matheus and C. G. Moreira). Using dynamical interpretation of these sets, in a joint work with M. Pollicott we developed a new method for computing their Hausdorff dimension.

The continued fraction is an alternative way to represent a real number as a limit of a sequence of rational numbers. Recall that for a real number α its continued fraction is an expression of the form

α  =

a0 +  1 a1 +  1 a2 +  1 a3 + ...

=  a0+1/(a1+1/(a2+1/(a3+...)))  =

[a0; a1, a2, a3, ... ]

The latter notation is due to Carl Friedrich Gauss. It is easy to see that the continued fraction is finite if and only if α is rational; and the sequence of partial denominators is periodic if and only if α is quadratic irrational. The Gauss map T: x ↦

1

x

−

[	1	]
	x

restricted to the interval (0,1) is acting on the sequence of partial denominators a_n by translation, forgetting the first element

T: [0;a₁,a₂,a₃...] ↦ [0;a₂,a₃,a₄...]

It is therefore not invertible, but has infinitely many inverse branches T_j : x ↦

1

x + j

, these are contractions acting on the compact interval [0,1]. On the sequence of partial denominators each T_j is acting by inserting the digit j:

T_j : [0;a₁,a₂,a₃...] ↦ [0;j,a₁,a₂,a₃...]

We may pick a pair of integers, say, 1 and 2 and consider an iterated function scheme of two inverse branches T₁,T₂. Then for any α∈[0,1] = [0;a₁,a₂,a₃...] and for any sequence {j_n} of 1s and 2s the images

T_jn...T_j3T_j2T_j1 : α= [0;a₁,a₂,a₃...] ↦ [0;j_n,...,j₃,j₂,j₁,a₁,a₂,a₃...]

converge to a number whose partial denominators are all either 1 or 2. The set of all such numbers has been well studied and even has a dedicated notation.

C₂ = {x ∈ (0,1) | x = [0; a₁, a₂, a₃, ... ],  where a_j = 1 or a_j = 2   for all indices j }.

It is a nonlinear Cantor set and it has a complex fractal structure. More generally, the sets which arise as limit sets of iterated function schemes of (a finite number of) the inverse branches T_j are called Gauss—Cantor sets. The Hausdorff dimension of C₂ has now been computed to very high accuracy and we give 200 digits of it in Section 4.1.2 of our paper. For practical applications it is useful to know that

dim_H C₂ = 0.53128... > 0.5.

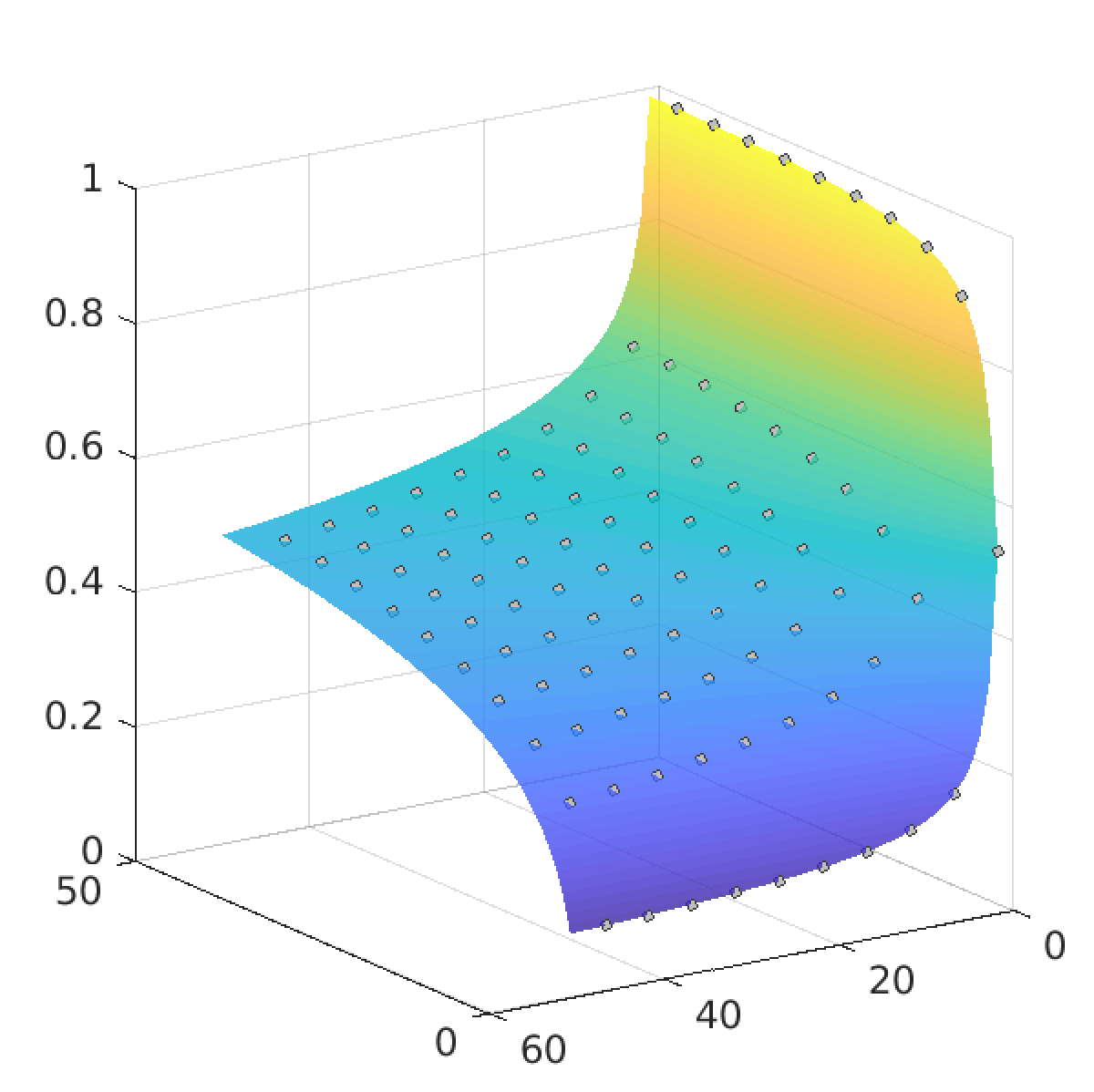
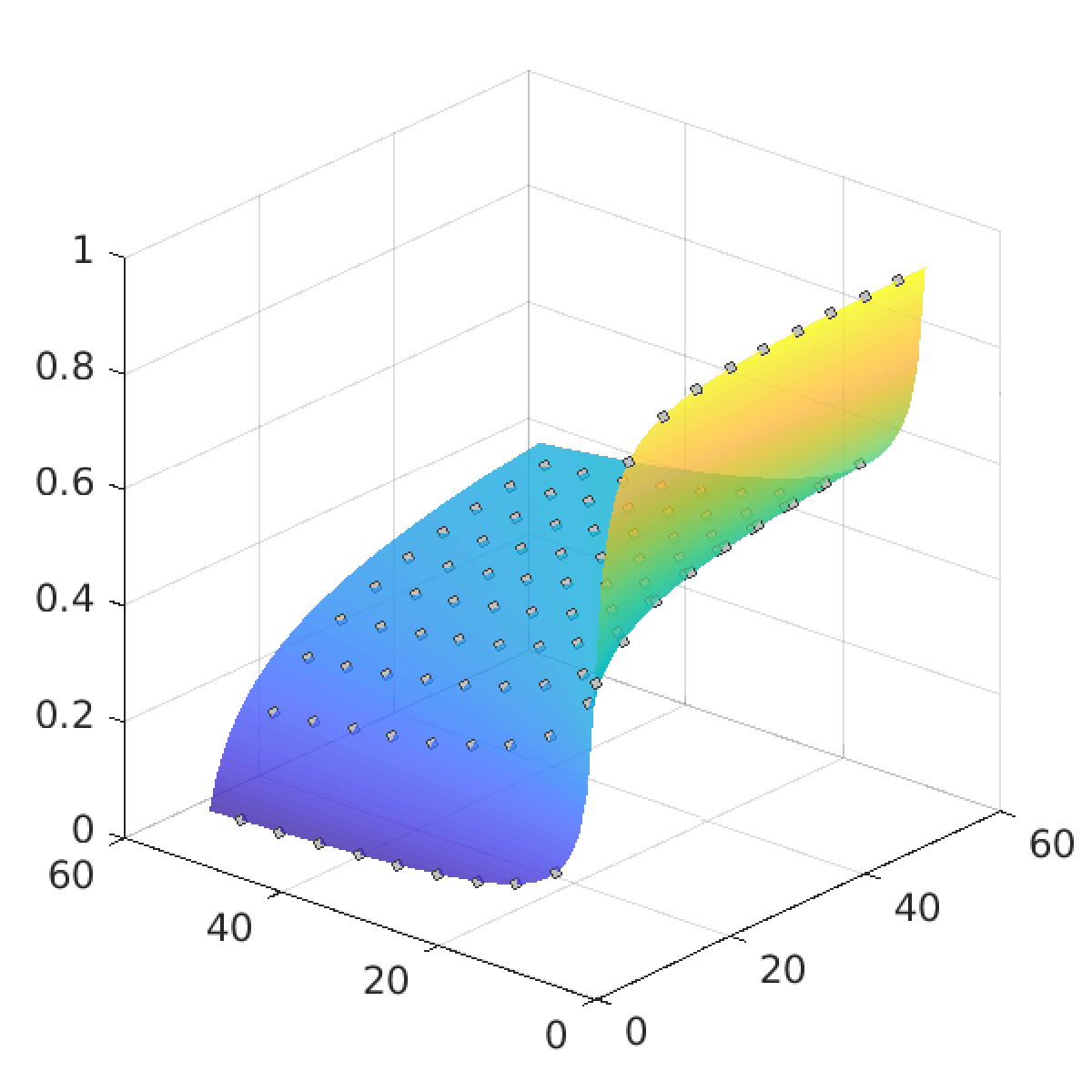
Figure 1 on the left depicts the dimension of a two-parameter family of sets

E_n,k = {x ∈ (0,1) | x = [0; a₁, a₂, a₃, ... ],  where a_j ∈ {n, n+1, ... , n+k}   for all indices j }

as a function of two variables d(n,k) = dim_H E_n,k for n,k = 1, ... , 50 . The set C₂ corresponds to the choices n = 1 and k = 1, so C₂ = E_1,1. The method we developed allows us to compute these 2500 values in just a few minutes with accuracy of 10⁻⁵. We see that for any fixed k₀ the function d(n,k₀) decreases rather rapidly as a function of n. For instance, in a special case k₀ = 1 with only two digits n and n+1 in the expansion, we get

d(2,1) = 0.3374... ,   d(3,1) = 0.2637... ,   d(50,1) = 0.0883....

On the other side of the parameter domain, when k₀ = 50 we have

d(1,50) = 0.9872...,   d(2,50) = 0.8085...,   d(50,50) = 0.4594....

Our algorithm enabled us to establish several estimates on the dimension of Gauss—Cantor sets, which are essential for the results on the density-one and modular forms of the Zaremba conjecture (pdf).

Continued fractions also appear in Diophantine approximation in connection with the Markov and Lagrange spectra. The Markov spectrum first appeared in 1879–80 in work by A. A. Markov (father) on quadratic forms. Later, Perron gave an alternative definition, in terms of continued fractions. On a set of bi-infinite sequences of natural numbers, we may define a real-valued function

λ : {a_n} ↦ a₀ + [0;a₁,a₂,a₃...] + [0;a₋₁,a₋₂,a₋₃...] ∈ R.

Then the Markov number of {a_n} is defined as a limit of the values of λ along the trajectory of the Bernoulli shift σ : {a_n} ↦ {a_n+1} , namely

m({a_n}) := lim_j→∞ λ(σ^j{a_n}).

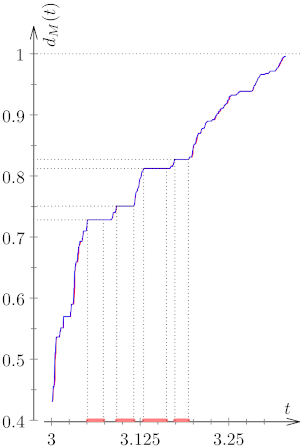
The (classical) Markov spectrum M is then defined as the set of all Markov numbers for all possible sequences of integers. It is known that (-∞,3) ∩ M is a discrete set and M ∩ (√21,+∞) is the entire ray. In the interval [3,√21] the Markov spectrum has rich fractal structure. Figure 2 on the left shows an approximation to the dimension of (-∞,t) ∩ M as a function of t. A recent result by C. G. Moreira shows that d_M(t)=dim_H((-∞,t) ∩ M) is a Cantor function, i.e. a continuous function which is locally constant on an open dense set. The approximation was calculated using the method we developed in our paper (joint with C. Matheus, C. G. Moreira and M. Pollicott), where we study other properties of the Markov spectrum and its closely related cousin called the Lagrange spectrum. The pink intervals show the gaps in the Markov spectrum, which are given, for instance, in the Cusick and Flahive’s textbook “Markov and Lagrange spectra” (published in 1991).