P-adic Hodge theory and Topological Hochschild Homology

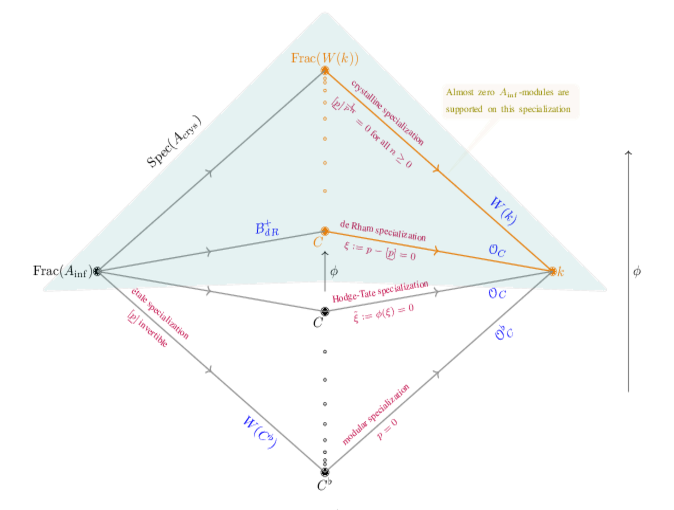
and various comparison isomorphisms relating these after scalar extension by huge period rings. In the paper [7] Bhatt-Morrow-Scholze proposed a new approach to the subject. Namely they constructed a functorial (in the higher categorical sense) complex $C^*({\frak X}, A_{inf})$ of perfect $A_{inf}$-modules, where $A_{inf}$ is the Fontaine's infinitesimal period ring (you can see the picture of $A_{inf}$ on the right) such that all other cohomology theories (up to a scalar extension) can be obtained by restricting $C^*({\frak X}, A_{inf})$ to various subsets of $\mathrm{Spec}\ A_{inf}$. Using that these subsets have non-empty intersections one obtains comparison isomorphism mentioned above. Moreover under torsion-freeness assumptions and using some additional input from abstract $p$-adic Hodge theory (Breuil-Kisin and Breuil-Kisin-Fargues modules) one can even recover crystalline cohomologies from etale ones without any scalar extension.

During our seminar we will try to understand construction of this new cohomology theory and various comparison results. More concretely:

• Adic and perfectoid spaces. The $A_{inf}$-theory is constructed almost (in the technical sense of the word) as follows: first for a perfectoid algebra $R$ (i.e. a $p$-torsion free $p$-complete commutative ring such that the Frobenius map $R/p^{1/p} \to R/p$ is an isomorphism) one sets by definition $C^*(\mathrm{Spf}\ R, A_{inf}) := A_{inf}(R) = W((R/p)^{perf})$ (i.e. perfectoid algebras are acyclic with respect to $A_{inf}$-cohomology theory). Now just as one can consider an algebraic variety over the complex numbers as a complex analytic object, to any (formal) scheme ${\frak X}$ as above one can associate its adic space ${\frak X}^{ad}$. Moreover by a theorem of Scholze every object in the category of adic spaces admits pro-etale covering by $(\mathrm{Spf}\ R)^{ad}$ for $R$ perfectoid. One then (almost) defines $C^*({\frak X}, A_{inf})$ as a (homotopy) limit of $A_{inf}(R)$ over all such coverings.

• $C^*({\frak X}, A_{inf})$ and classical cohomology theories. In order to relate $C^*({\frak X}, A_{inf})$ to other cohomology theories one constructs a complex of sheaves of $A_{inf}$-modules $A\Omega_{\frak X}$ in Zariski topology on ${\frak X}$ such that $\Gamma({\frak X}_{Zar}, A\Omega_{\frak X}) \simeq C^*({\frak X}, A_{inf})$. Using some hard local computations it is then possible to show that $A\Omega_{\frak X}$ admits a filtration by complexes $\widetilde{W_r\Omega_{\frak X}}$, such that $\mathcal H^*({\frak X}_{Zar}, \widetilde{W_r\Omega_{\frak X})}$ are given by $r$'s de Rham-Witt complex of ${\frak X}$, which allows to relate $A\Omega_{\frak X}$ to (continuous) de Rham complex of ${\frak X}$ and a complex which computes crystalline cohomology of ${\frak X}$. The most non-trivial comparison is with etale cohomology which heavily relies on Scholze's results about $p$-adic Hodge theory for rigid-analytic varieties [9] and Huber's work on the etale cohomology of adic spaces.

• Topological Hochschild Homology. Hochschild Homology of an associative algebra $A$ over a commutative ring (spectrum) $k$ are defined as the (derived) tensor product $A \otimes_{A \otimes_k A^{op}} A$. Topological Hochschild Homology $THH(A)$ is just the Hochschild Homology of $A$ for $k$ being the sphere spectrum. After the work Connes it is well-known that Hochschild Homology admits a homotopy circle action. In fact in the case when $A$ is of positive (or mixed) characteristic $THH(A)$ admits a reacher structure of a so-called cyclotomic spetrum, which is (at least in the case when $A$ is connective) by definition an $\mathbb S^1$-equivariant spectrum together with the choice of $\mathbb S^1$-equivariant "Frobenius" morphisms $THH(A) \to THH(A)^{tC_p}$ for every prime $p$. It turns out that $A_{inf}$-theory is closely related to $THH$: namely by the result of Hesselholt the homotopy groups of topological Frobenius homology $TF(\mathcal O_C)$ are given by $A_{inf}[\sigma]$ with $\deg(\sigma) = 2$. More generally for ($p$-adic completion of) a smooth algebra $R$ over $\mathcal O_C$ there is a close relation between $\pi_* THH(R)^{C_{p^r}}$ and the complex $\widetilde{W_r\Omega_{\frak X}}$ mentioned above. We will review the theory of cyclotomic spectra after the work of Nikolaus-Scholze [13], relations between $THH$ and $A_{inf}$-cohomology and the original application of $THH$ to algebraic $K$-theory of nilpotent extensions (Goodwillie-Dundas-McCarthy theorem).

Plan

1. Adic spaces, perfectoid spaces, diamonds.
2. A_inf, tilting equivalence. Fargues-Fontaine curve.
3. Pro-etale site, some almost mathematics.
4. Elements of rational p-adic Hodge theory. Breuil-Kisin-Fargues modules.
5. Reminder of crystalline cohomology theory, de Rham-Witt complex.
6. Construction of A_inf-cohomology theory via nearby cycles. Comparison with etale and crystalline cohomology. Applications.
7. Cyclotomic spectra. Topological Hochschild and Cyclic Homology. Hopkins-Mahowald theorem. THH of group algebras and Thom spectra.
8. A\Omega and THH. Hesselholt-Madsen theorem. Motivic filtration.
9. Reminder of algebraic K-theory: Waldhausen's S-construction, K-theory and THH as additivizations of core groupoid and endomorphism functors respectively. Cyclotomic trace map.
10. Goodwillie's calculus of functors, Goodwillie-Dundas-McCarthy theorem.

Talks

References

Backgroud material on adic and perfectoid spaces

1. Arizona Winter School 2017: Perfectoid Spaces.
2. Peter Scholze, Jared Weinstein, Lectures on p-adic geometry.
3. Peter Scholze, Perfectoid spaces.
4. Bhargav Bhatt, Peter Scholze, The pro-etale topology for schemes.
5. Roland Huber, Etale Cohomology of Rigid Analytic Varieties and Adic Spaces.

   P-adic Hodge Theory

6. Jean-Marc Fontain, Representations p-adiques des corps locaux.
7. Mark Kisn, Crystalline representations and F-crystalls.
8. Olivier Brinon, Brian Conrad, CMI summer school notes on p-adic Hodge theory.
9. Bhargav Bhatt, Matthew Morrow, Peter Scholze, Integral p-adic Hodge theory.
10. Bhargav Bhatt, Specializing varieties and their cohomology from characteristic 0 to characteristic p.
11. Peter Scholze, p-adic Hodge theory for rigid-analytic varieties.
12. Alexander Beilinson, Floric Tavares Ribeiro, On a theorem of Kisin.

    Hochschild Homology and K-theory

13. Thomas G.Goodwillie, Cyclic homology, derivations, and the free loopspace.
14. Clark Barwick, On the algebraic K-theory of higher categories.
15. Ib Madsen, Algebraic K-theory and traces.
16. Bjorn Ian Dundas, Thomas G. Goodwillie, Randy McCarthy, The local structure of algebraic K-theory.
17. Thomas Nikolaus, Peter Scholze, On topological cyclic homology.
18. Lars Hesselholt, Ib Madsen, On the K-theory of finite algebras over Witt vectors of perfect fields.
19. Bhargav Bhatt, Matthew Morrow, Peter Scholze, Topological Hochschild homology and integral p-adic Hodge theory.
20. Akhil Mathew, Kaledin's degeneration theorem and topological Hochschild homology.
21. Dustin Clausen, Akhil Mathew, Matthew Morrow, K-theory and topological cyclic homology of henselian pairs.
22. Sam Raskin, On the Dundas-Goodwillie-McCarthy theorem.

Back to Artem Prikhodko's home page.